ESOEA: Ensemble of Single Objective Evolutionary Algorithms for Many-Objective Optimization

Authors: Monalisa Pal and Sanghamitra Bandyopadhyay
Email: monalisapal_r@isical.ac.in and sanghami@isical.ac.in
Link to publication: https://doi.org/10.1016/j.swevo.2019.03.006

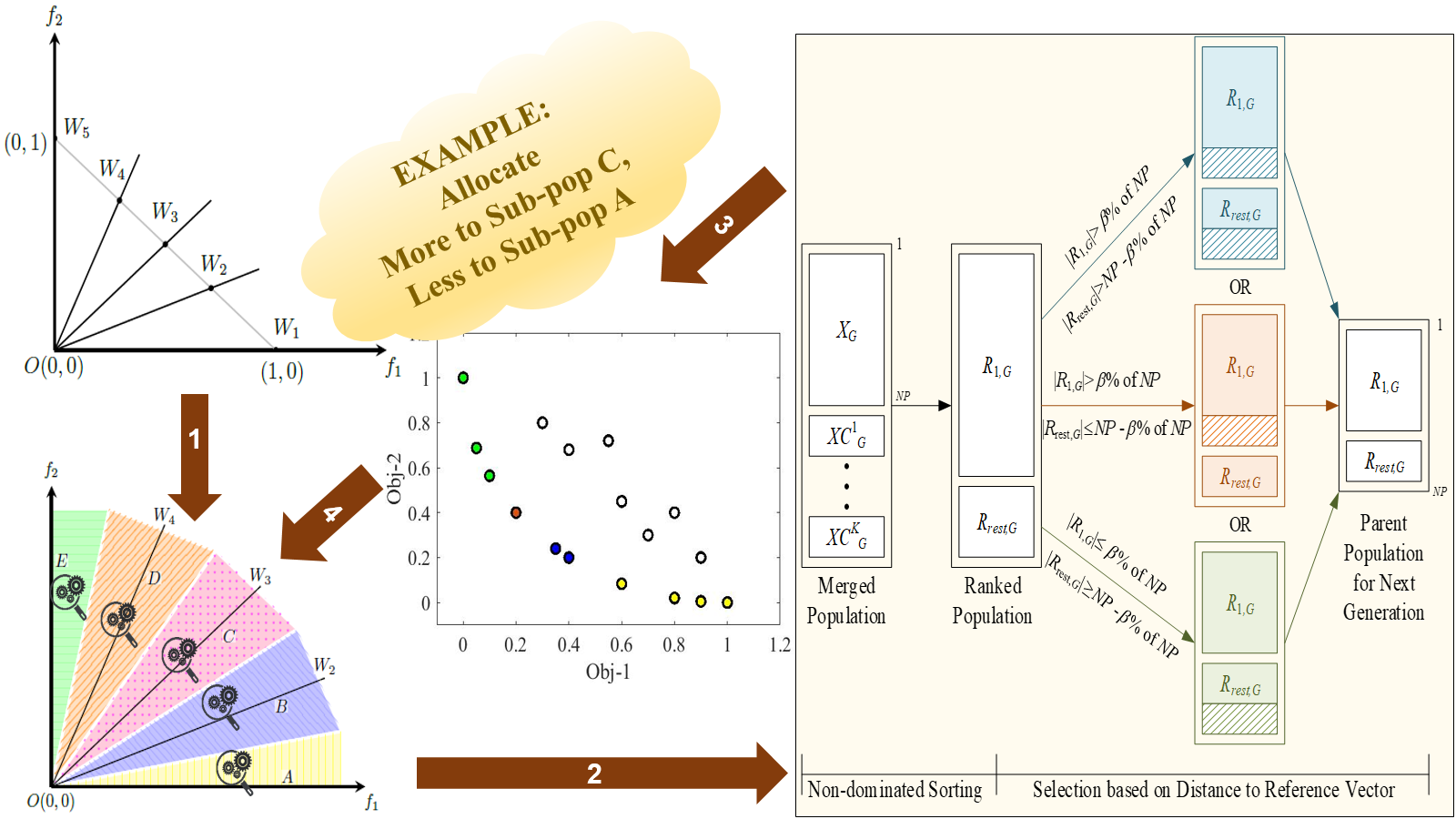
Welcome to this webpage which presents a many-objective optimization approach viz. ESOEA or Ensemble of Single Objective Evolutionary Algorithms. Its novel highlights of adaptive feedback and regulated elitism make it robust to handle problem characteristics such as multiple modalities, biased density of solutions, disconnected Pareto-fronts, Pareto-fronts with sharp tails, imbalance difficulties and difficulties associated with variable linkage. This proposed algorithm has been applied on DTLZ, WFG, IMB and CEC 2009 test problems and the efficacy of the approach has been analysed using IGD metric, hypervolume indicator, convergence metric and visualization of Pareto-fronts. An illustrative flow of the proposed approach is shown in the figure below. This webpage also contains a supplementary material for describing an alternate weight distribution scheme which can be beneficial to regulate the complexity for problems with large number of objectives.

An alternative weight distribution strategy

An alternative method of distributing weight vectors is available for downloading as the supplementary material in the file named "Supplementary.pdf". This method aids the reference direction associated many-objective optimization algorithms for defining the reference directions. Specifically, the supplementary material provides the following information:

1. the motivation for exploring an alternative weight distribution strategy
2. the proposed approach to address this concerned problem, and
3. performance analysis of various experiments to validate this alternative weight distribution approach.

Click here to download the supplementary material.

Specifications of the code

The code for ESOEA/DE is compatible with MATLAB R2018a and a system having Intel Core i7 processor @ 2.2GHz and 8GB RAM.

The MATLAB codes are available in a compressed folder named "ESOEA.zip" which is downloadable from the link below. The compressed folder is to be extracted in which there are 26 .m files, 6 .mat files and a folder named "Results". Out of these .m files, the file named "main.m" is to be executed and all the remaining ones are function definitions required for the entire execution.

Click here to download the MATLAB codes.

As ESOEA is a decomposition-based approach, the implementation is available with standard settings of sub-space partitioning. For any arbitrary sub-space partitioning, please visit this page.

Steps to execute the associated program

The code can be executed as listed below. Against each step, a screenshot is provided for reference. The screenshots are taken during execution of the code in Windows 10.

1. Open MATLAB. (Here, MATLAB R2018a has been used.)
2. Use the drop-down arrow (highlighted by green box) to browse to the location (highlighted by red box) where the ZIP folder has been extracted. Ensure there are 32 files and 1 folder in the location from the "Current Folder" pane, including the file named "main.m" (highlighted by purple box) which is the file to be executed.
3. One of the ways to execute the file (main.m) is to open the file in an Editor window (by double-clicking "main.m" under "Current Folder" pane) and use the "Run" button of the Editor window (highlighted by red box). Alternatively, one can type the filename i.e. main in the "Command Window" when the prompt (>>) appears in order to execute the program.
4. Enter the information asked in the "Command Window" (highlighted by red box). Note that all the previously entered commands can be seen from the "Command History" pane (highlighted by purple box).
5. After all the user-inputs are provided, ESOEA/DE algorithm starts to search for the Pareto-optimal set of solutions.
6. At the end of the program execution, a plot appears in a separate window called "Figure 1". "Figure 1" shows the estimated Pareto-Front for the DTLZ test problem under consideration, as estimated by ESOEA/DE. Beside the plots, the optimization results (i.e. hypervolume, convergence, IGD and number of points in the estimated Pareto-front) appear in the "Command Window". For each run, 3 files are created in the "Results" folder (highlighted by green box) where the objective values, the performance values and the plot of the estimated Pareto-Front are saved.

1 / 6

Step 1 of 6

2 / 6

Step 2 of 6

3 / 6

Step 3 of 6

4 / 6

Step 4 of 6

5 / 6

Step 5 of 6

6 / 6

Step 6 of 6

❮ ❯

Links to Other Projects

• DECOR: Differential Evolution using Clustering based Objective Reduction for Many-Objective Optimization
• Code and data for sub-space partitioning (for decomposition-based EAs)
• NAEMO: Neighborhood-sensitive Archived Evolutionary Many-objective Optimization Algorithm
• Unmasking the causal relationships latent in the interplay between occupant's actions and indoor ambience: a building energy management outlook
• Uniform Distribution driven Adaptive Differential Evolution